Polyhedra in Knots
Celtic knots, or interlace, are a beautiful, ancient art form with interesting symmetries and topological properties:

It turns out that you can follow a recipe to turn any planar graph into its corresponding knotwork, or vice-versa. (You can follow this recipe, the Mercat procedure, by hand; alternatively, it's precise enough that you can implement it as a computer program.)
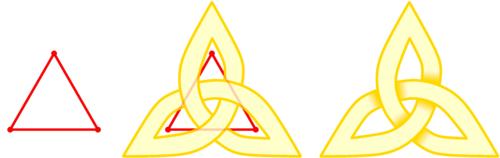
Figure 2: You can transform any graph into knotwork. (entrelacs.com)
With this recipe in hand, I began seriously wondering what some of my favorite and familiar graphs would look like as knotwork. What about the triforce symbol? Or a square? What about a cube? Oh! And what about the rest of the platonic solids as well?
 |
 |
 |
 |
 |
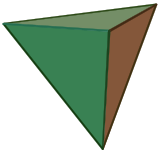
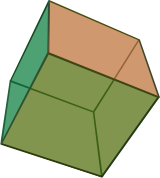
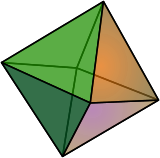
Yes, that was a good challenge. The platonic solids are fun to try to visualize (I hadn't learned how to effectively visualize yarn wrapping around 3D shapes, so I had to try several ways of drawing them in two-dimensional flatland; see below.). After much trial and error, I got the following glorious series of pictures:
 |
tetrahedron | 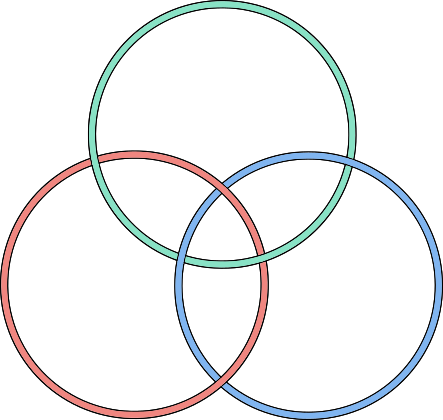 |
 |
cube | 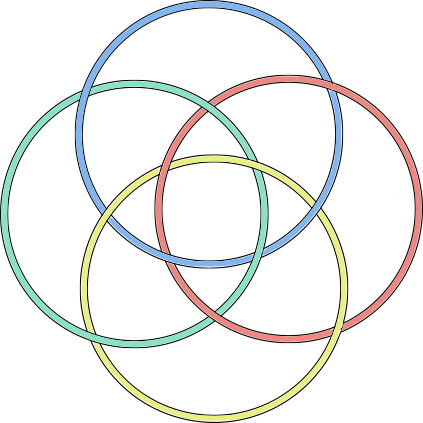 |
 |
octahedron | 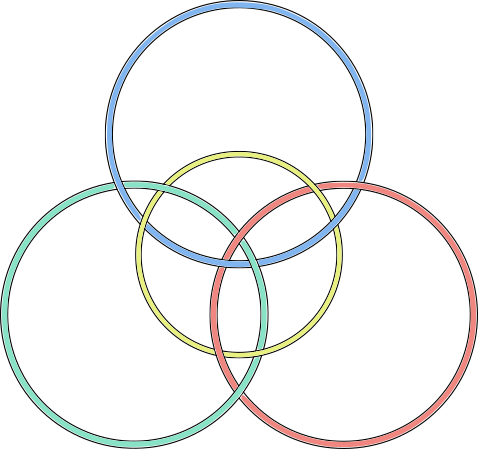 |
 |
dodecahedron |  |
 |
icosahedron |  |
As you can see here,
- Each knotwork consists of interlocked circles (3 for the tetrahedron; 4 for the cube and octahedron; 6 for the dodecahedron and icosahedron).
- Corresponding pairs of dual shapes have the same number of circles (cube-octahedron, dodecahedron-icosahedron). They vary based on how the circles are arranged; e.g. whether there's a central circle.
- Each knotwork has various symmetries including rotational and reflective, as well as the over-under pattern of string crossings.
- The overlapping circles create regions with recognizable shapes. For example, the icosahedron's knotwork is made up of five-sided and three-sided regions (with a pentagon in the middle). Its dual, the dodecahedron, is made of the same shapes, but with a triangle in the middle. You can see these shapes more clearly when the regions are colored in a checkerboard pattern (see below). The cube and octahedron include four-sided regions.
- There are other patterns if you look—for example, how many stars can you spot in the icosahedron and dodecahedron knotwork below?
 |
tetrahedron |  |
 |
cube |  |
 |
octahedron |  |
 |
dodecahedron |  |
 |
icosahedron |  |

Mathematical remark: To count the number of threads, you can use the formula: \(|T(-1,-1)| = 2^{c-1}\) where T is the Tutte polynomial of the planar graph, and c is the number of threads. Incidentally, because the dual of a graph has the same Tutte polynomial with x and y exchanged, this implies a full generalization of the result we discovered here: every graph has the same number of knotwork strands as its dual.
Mathematical remark: As shown in the checkerboard-shaded pictures, the knotwork for each polyhedron divides space into two kinds of shape, e.g. triangles and pentagons. The two shapes are apparently directly related to the Schlaffi symbol for the polyhedron—that is, the shape of each face, and the number of faces meeting at each vertex.
1 How I generated these
To generate this knotwork, you start with one of the figures such as
the icosahedron:
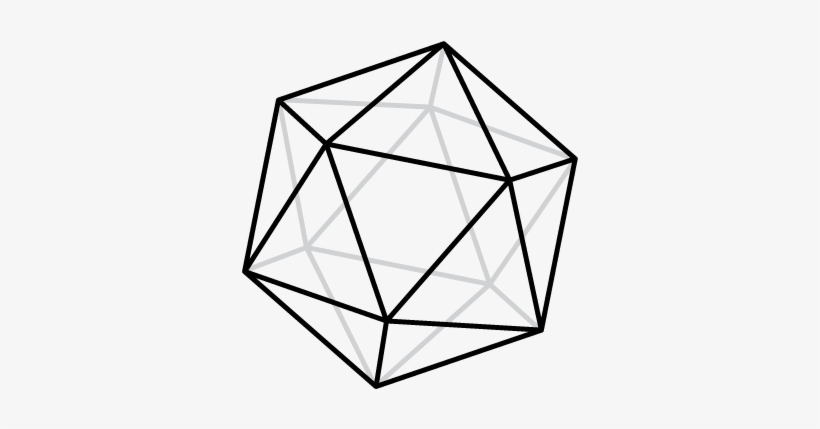
You want to stretch it so that you can draw it on a flat piece of
paper without any of the lines crossing. In this particular case, you
can take the back-face triangle and pull all of its vertices out from
behind the icosahedron. The result is a planar graph:
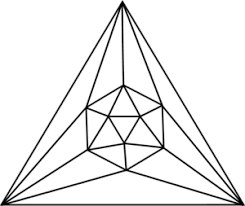 .
.
Now we can apply the Mercat procedure to draw threads that cross in pairs at the midpoint of every edge in the graph. The result is a bit messy, but if you color in each of the threads in a different color, you see that the knotwork is made up of simple (non-self-intersecting) closed loops.
To straighten out the wobby loops into perfect circles, all I did was arrange some colored circles by trial and error into positions that had the same symmetry as the knotwork. I then checked whether my circles had the same crossings as the knotwork, and made the same shaped regions (triangles, pentagons). The result is as you've seen, and you can repeat this process for any of the other polyhedra:

2 Show your work
What follows is a gallery of my handwritten drawings on the subject, because I think they look interesting, and might be enjoyable or useful to see:
It was a bit of a struggle for the imagination at first, chasing threads around the corners of polyhedra and visualizing where they would end up. The problem was only partially solved by unfolding the polyhedra, because then threads that vanished off one side of the figure would appear on another in a seemingly different orientation. Eventually, I discovered that I could represent the edges of the graph and their "shares vertex" relationships as graphs themselves. These graphs were all planar, and simplified the Mercat procedure terrifically.
I chose polyhedra at random, discovering a pattern: all of their knotwork seemed to consist solely of overlapping circles:
tetrahedron: 3 circles cube: 4 circles octahedron: ___ dodecahedron: 6 circles icosahedron: __
What's the pattern? Imagine my surprise when I drew out the knotwork for the rest and found out that the pattern was:
tetrahedron: 3 circles cube: 4 circles octahedron: 4 circles (!) dodecahedron: 6 circles icosahedron: 6 circles (!)
The knotwork for the cube and octahedron was identical, as was the knotwork for the dodecahedron and the icosahedron! In retrospect, these relationships are less mysterious in light of dual polyhedra: the cube and octahedron are dual pairs, as are the dodecahedron and the icosahedron. This means, in part, that if you draw lines to connect the faces of one shape, you get the dual shape. (The tetrahedron, on its own, is self-dual.)
(I wonder if we can state the proof that there are only five platonic solids in terms of the number of circles that a hypothetical platonoic solid would have in its knotwork, and how those circles would overlap?)
Tetrahedron. Here, I use my abstract method to draw the knotwork for the tetrahedron. Each node in the graph represents a pair of faces (an edge of the polyhedron), and each edge in the graph represents a shared-vertex relationship. The edges are oriented at various multiples of 45 degrees, as they must be lined up in the final knotwork.
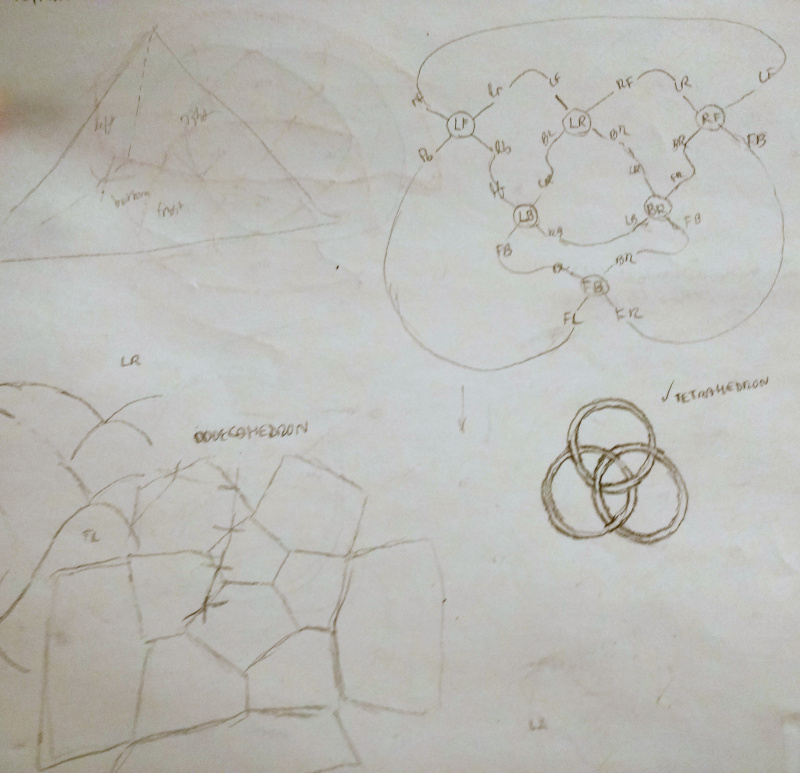
Cube. The cube was the first shape I attempted, actually. You can see in the bottom left, I attempted to visualize the movements of the threads in 3D. When I looked for a simpler method, I tried unfolding the cube and having the threads "wrap around" as needed (upper-left cross-like figure). The apparent orientation changes (in the 2D unfolding) made this method a bit difficult. On the right right, I begin to wonder whether I can represent the knotwork as overlapping circles.
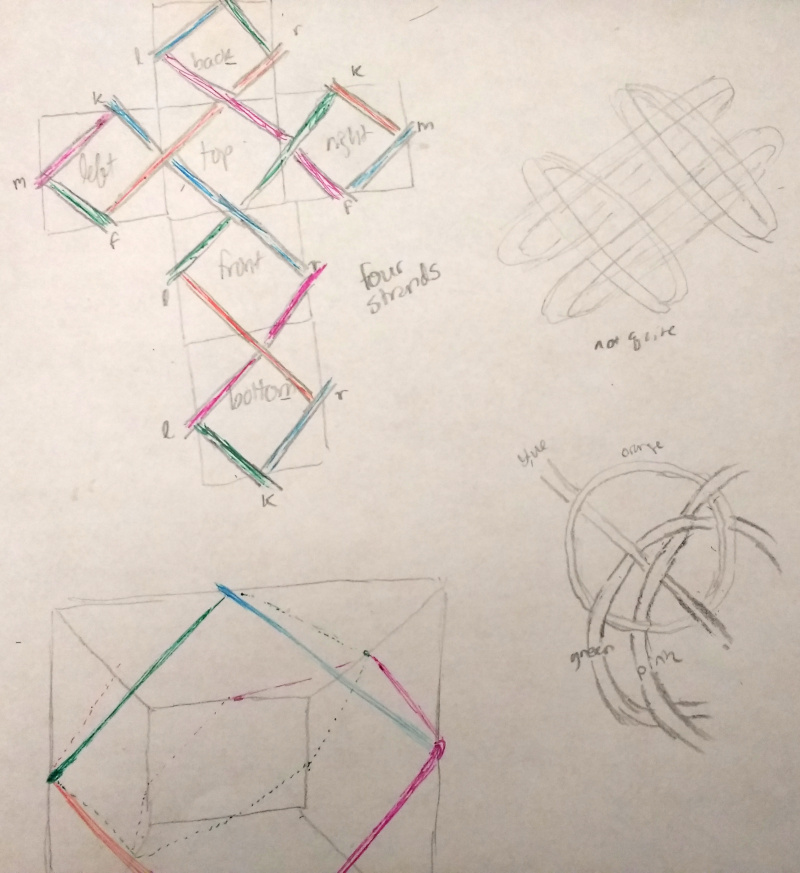
Cube #2. Following my initial hunch about overlapping circles…
…I eventually succeed at drawing the cube's knotwork (four interlocking circles in upper-right), using the abstract method I developed on the simpler tetrahedron (note some stray tetrahedron attempts around the bottom-left periphery). I rather like the teardrop-shaped aesthetic of the middle incarnation, but the four interlocking circles are more symmetric.
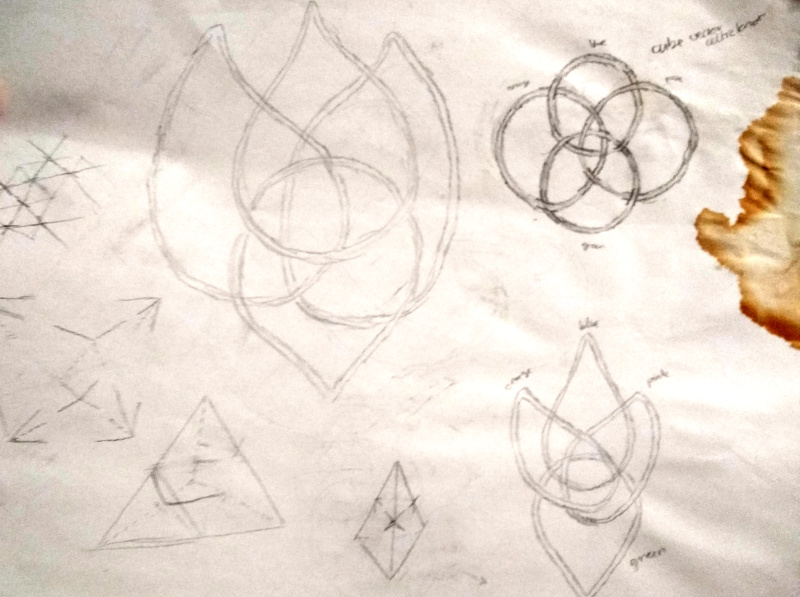
Dodecahedron. The dodecahedron was a real challenge, moving from the planar graph shown here (with all its intricate thread crossings, two per edge)…
… to the final, stunning result:
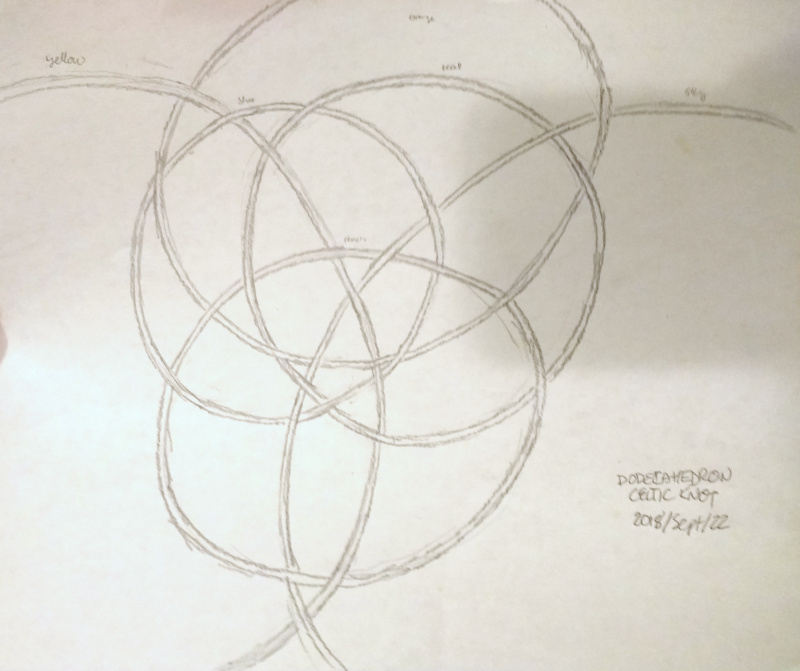
Icosahedron I initially attempted the icosahedron's knotwork using the "unfolding" method with its bewildering wrapped threads:
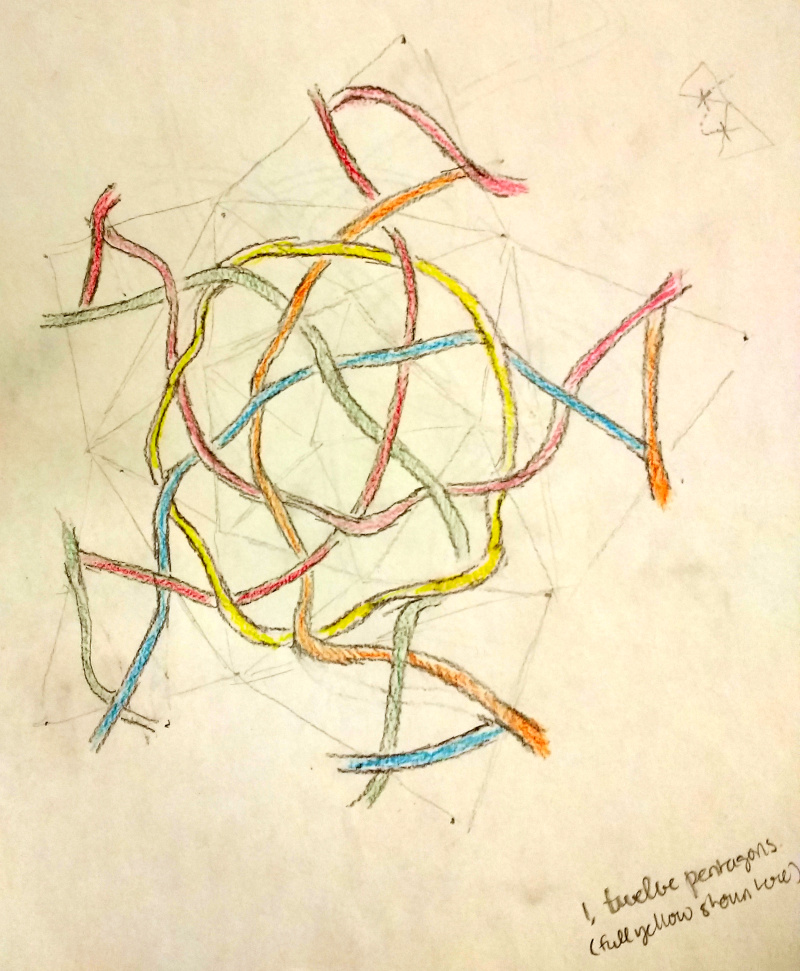
Eventually, I discovered the abstract method (and the duality principle), and the rest is exactly the same as for the dodecahedron, shown here again (notice the star shape in the middle of the two figures here? They're overflowing with star-shaped intersections of threads if you look!):
